A braid applet, explanations

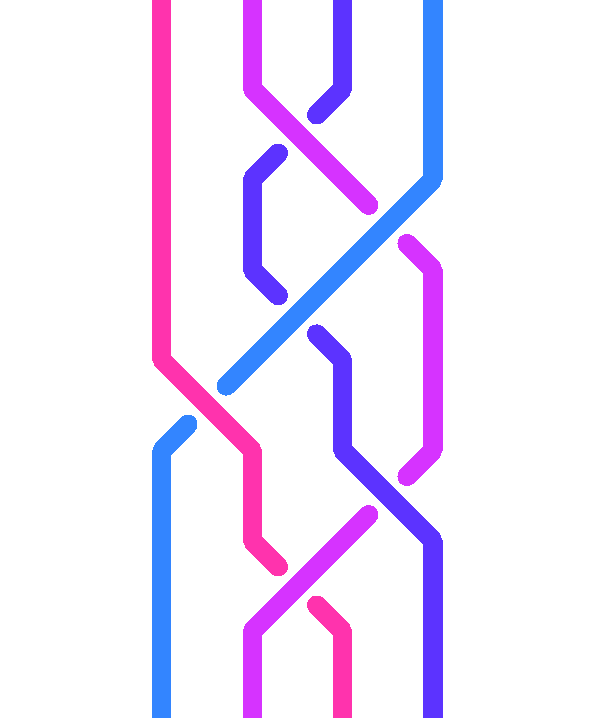
A braid diagram is a picture consisting of strands that cross, on the shape of

In order to describe a braid diagrams, we can encode it using a braid word, i.e., a finite sequence of letters 'a', 'A', ..., 'z', 'Z'. When considered from top to bottom, a braid diagram consists of a finite succession of crossings. In order to describe it, it is sufficient to specify the successive crossings, hence to say which strands cross, and with which orientation. Traditionally, one numbers the positions from 1 to n in an n strand braid diagram, and one calls a (or σ₁) the crossing where the strand at position 2 crosses over the strand at position 1, then b (or σ₂) the crossing where the strand at position 3 crosses over the strand at position 2, etc. Symmetrically, we shall use A (or σ₁^-1) for the crossing where the strand at position 1 crosses over the strand at position 2, then B (or σ₂^-1) the crossing where the strand at position 2 crosses over the strand at position 3, etc.

a    →        ,  A    →    

b    →        ,  B    →    

Two n braid diagrams are said to be isotopic if they are projections of two 3-dimensional figures that can be continuously deformed one into the other, i.e., one can go from the former to the latter by moving the strands, but keeping the ends fixed and not allowing one strand to pass through another one. For instance, the diagrams below are isotopic, as the animation shows.

    =        =    

    =        =    

The Braid Isotopy Problem is neither very easy, nor very difficult. It has been solved for the first time by the mathematician Emil Artin in the 1930's. Today, many different solutions are known, actually more than a dozen. They relie on various approaches, but all require relatively sophisticated results about braids. Below, we describe one such solution called handle reduction.

One says that a braid diagram is trivial if it is isotopic to a diagram with no crossing at all. The Braid Triviality Problem is the algorithmic problem:

Yes, they are indeed equivalent problems. Firstly, the Braid Triviality Problem is a special case of the Braid Isotopy Problem, so each solution to the latter automatically gives a solution to the former. On the other hand, one can easily check that, if D and D' are n strand braid diagrams, then D and D' are isotopic if and only if the braid diagram D'' obtained by stacking the image of D in a horizontal mirror over D is trivial. Thus, any solution to the Braid Triviality Problem leads to a solution to the Braid Isotopy Problem.

Handle Reduction is one of the many ways to solve the Braid Triviality Problem, i.e., to decide whether the braid diagram encoded by a given braid word can be deformed into a diagram with no crossing. Owing to the above remark, Handle Reduction also provides a solution to the Braid Isotopy Problem. Handle Reduction turns out to be extremely efficient in practice: when properly implemented, it enables one to compare diagrams involving thousands of crossings in less than one second.

A handle is a braid word of a special type. For s be any lower case letter (thus one of a, b, ...), let us define a s-handle to be a braid word of the form s...S, where S is the upper case letter associated with s and all intermediate letters between s and S are letters lying before s in alphabetical order. Symmetrically, for S an upper case letter, a S-handle is defined to be a braid word of the form S...s, where s is the lower case letter associated with S and all intermediate letters are before s in alphabetical order. Geometrically, a handle encodes a diagram in which the first and the last crossings have opposite orientations, and all intermediate crossings (if any) are located on the left of the first and the last crossings. For instance, the word cbAC is a c-handle, corresponding to the diagram

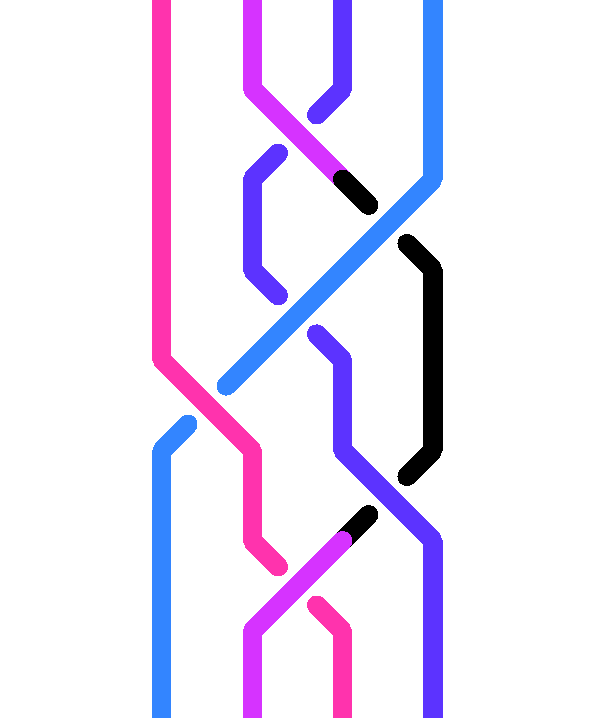
The principle of Handle Reduction is to try to get rid of handles. The basic step is an operation that transforms a handle into an equivalent word, called its reduct.
Assume that h is a s-handle. The reduct of h to be the braid word obtained from h by deleting the initial letter s and the final letter S, and, denoting by r the letter that lies immediately before s in alphabetical order and by R the associated upper case letter, by replacing every r in h (if any) with Rsr and every R in h (if any) with RSr. Symmetrically, if h is a S-handle, we define the reduct of h to be obtained from h by deleting the initial S and the final s, and replacing every r in h with rsR and every R in h with rSR, where r and R still denote the letters just before s in alphabetical order.
For instance, the reduct of the c-handle cbAC is BcbA, while the reduct of the A-handle Aa is the empty word.
Geometrically, the diagram encoded by the reduct of h is obtained from the diagram encoded by h by pushing to the left the strand that makes the handle, so that it skirts on the left of all neighbouring crossings.

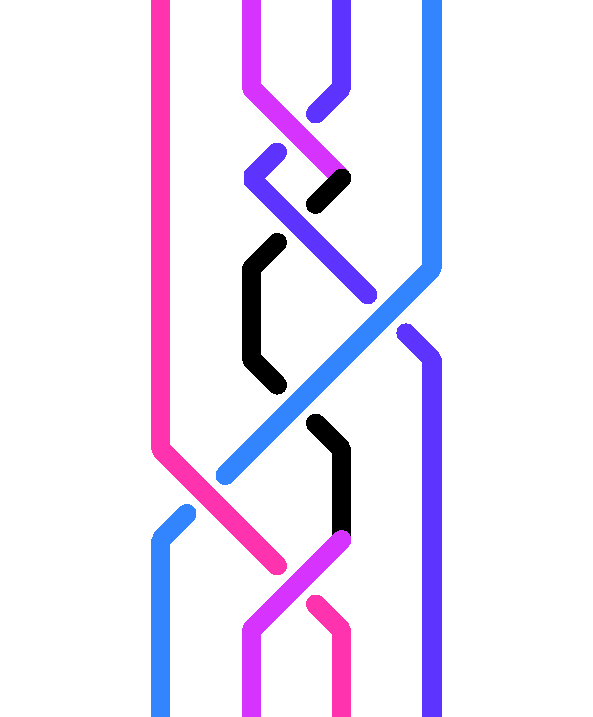
One starts with an arbitrary braid word w, one looks at the first handle in w, we reduce it, i.e., we replace the handle by its reduct, and we repeat the process with the new word so obtained until no more handle exists. Then we conclude as follows:

This is the hard point. A priori, it might very well happen that we continue reducing handles for ever, or that a word containing no handle be equivalent to the empty word. Actually, this never happens, so the Handle Reduction algorithm always converges and solves the Braid Triviality Problem. But this is a rather difficult result whose only proof known so far requires sophisticated mathematical methods. The main reason behind the correctness of the Handle Reduction algorithm is the existence of a certain braid ordering. For more details and explanations, see